Merhaba sevgili Bilgeyik okurları, bugünkü yazımızda dün İnstagramda sorduğumuz sorunun cevabını verecek ve İntegralin ne olduğu, ne işe yaradığı sorusunu yanıtlamaya çalışacağız. Yazının anlaşılır olması için okuyucadan bazı konulara hakim oluması beklenmektedir. Bu konular şunlardır:
- Fonksiyonlar
- Limit
- Türev
Şayet fonksiyonlar konusuna hakim değilseniz buradan "Fonksiyon nedir?" adlı yazıma, buradan da hem Türev hem de Limit konuları hakkında temel bilgilere sahip olabileceğiniz "Türev nedir?" adlı yazıma ulaşabilirsiniz.
İntegral nedir?
Bir şey eğer felsefenin ilgi alanına giriyorsa birçok tanımı bulunabilir ama bilimin alanına giriyorsa ve özellikle bu bilim dalı matematikse tanımı genellikle kısa ve nettir. Ben bugün daha önceki yazılarda da yaptığım gibi bu kısa ve net ama belirli bir bilgi birikimi yoksa anlaşılması güç tanımları kullanmayacağım; onun yerine anlaşılır olma ve okuyucunun ilgisini çekme, okuyucuda merak uyandırma amaçları taşıyan tanımlar kullanacağım.
İntegral her şeyden önce asla türevin tersi değildir. Türevin tersine "Ters türev" işlemi denir, ters türev ise integralde kullanılan bir işlemdir. Nasıl? Açıklayalım. İlk önce sorumuzu hatırlayalım.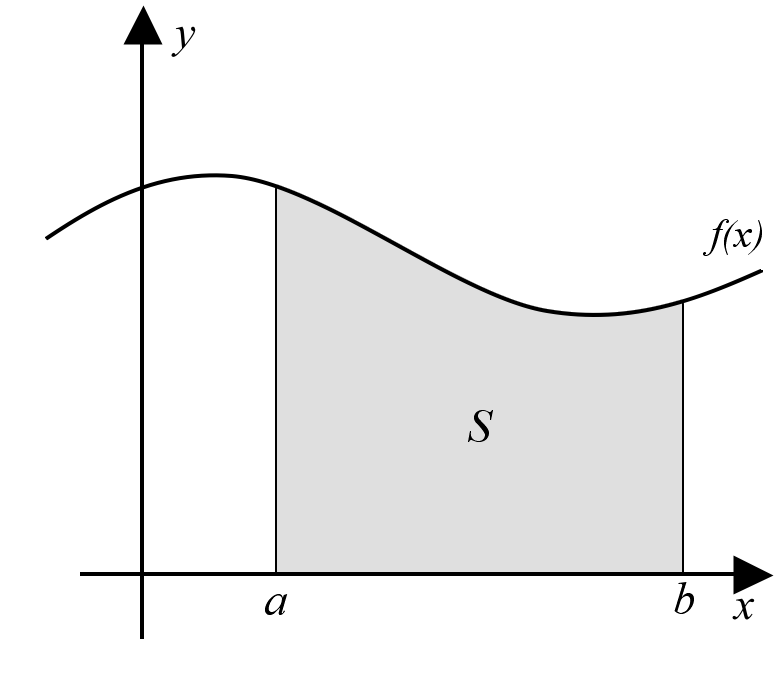
Yukarıdaki grafikte bir f(x) fonksiyonunu görmekteyiz, fonksiyon eğrisi ve a ile b sınırları arasında kalan, yani S ile gösterilen alanı nasıl bulabiliriz? Hepimiz düzgün şekilli geometrik cisimlerin alanını bulmayı biliyoruz, ama sanki yukarıdaki alanı bulmak için bu bilgilerimiz yeterli değil. Gelin beraber akıl yürütelim.
Riemann toplamı
Bu tarz bir şeklin alanını nasıl hesaplayacağımızı bilmiyoruz ama ya bildiğimiz şekillerden yola çıkarsak? Yani S alanının içinde dikdörtgenler çizersek ve onları toplarsak ne olur? Mesela aşağıda başka bir şekil var ama aynı mantıkla içine dikdörtgenler çiziliyor.

İlk dikdörtgen çiziminde alanda boşluklar kaldığını ve dikdörtgenlerden yola çıkarak hesapladığımız alanın S'in gerçek alanından daha küçük olduğunu fark etmişsinizdir. Dikdörtgen sayısı arttıkça S alanındaki boşluklar azalıyor. Bu da demektir ki ne kadar çok dikdörtgen çizersek gerçek alana o kadar çok yaklaşıyoruz. Limit konusuna hakim olanların kafasında burada bir ampül yandığını hissedebiliyorum :) Peki en fazla ne kadar dikdörtgen çizebiliriz? Kalem kağıtla yapılan çizimle değil de matematiksel işlemlerle ilerlesek, yani her çizilen dikdörtgenin enine x diyip, tüm ifadeleri matematiksel işlemlere döksek ve limitle x'i sonsuza götürsek; gerçek alana yaklaşabilir, S'in gerçek değerini bulabilir miyiz? Evet.
İşte bu x'i, yani kabaca dikdörtgen sayısını sonsuza götürdüğümüzde ve matematiksel işlemleri yaptığımızda karşımıza çıkan sonuç fonksiyon eğrisi ile x ekseni ve a ile b noktaları arasında kalan alandır. İntegral de bu işlemlerin fonksiyonel halidir. Aşağıda solda İntegral işaretini sağda ise çoğunuzun bildiği Toplam işareti var. İntegral sembolü Toplam işaretinin biraz değiştirilmiş halidir. Bunun sebebi de sizin de yukarıdan, yani dikdörtgenlerin toplamından fark edebileceğiniz gibi İntegralin "Toplam" ile ne kadar alakalı olduğuyla ilgilidir.

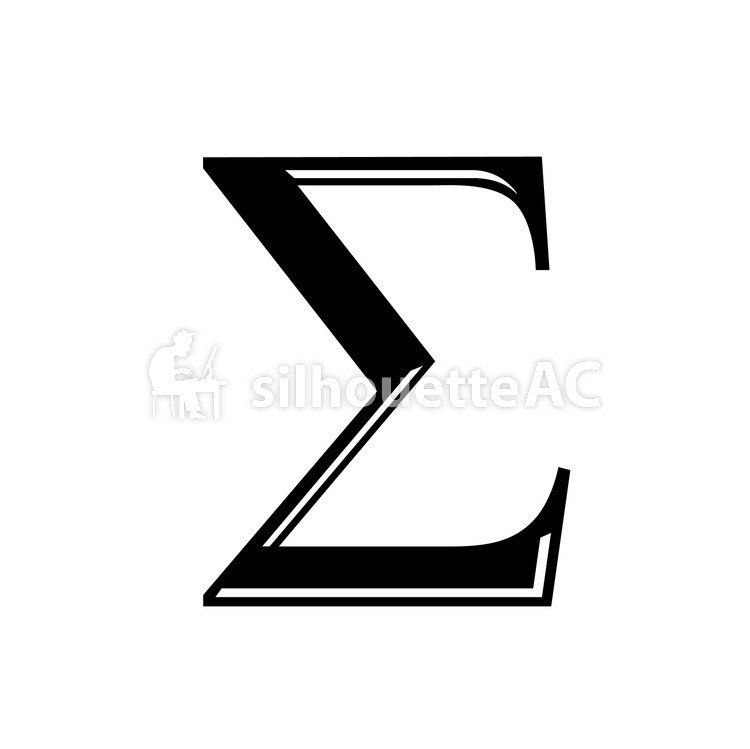
Yukarıda yaptığımız toplama işine Riemann toplamı denir, ismi bu işlemi yapan Bernhard Riemann'dan almıştır. Bernard Riemann daha birçok alanda birçok katkıları olan Alman matematikçidir.

Sonuç olarak
Sonuç olarak İntegral birçok farklı yolla anlatılabilir, basitleştirilebilir veyahut zorlaştırılabilir ancak asla "Türevin tersi" şeklinde bir anlatımı hak etmez. Sorduğumuz sorunun cevabı "İntegral"dir ve aşağıdaki gibi gösterilir.

Buradaki f ve F fonksiyonlarını karıştırmamak gerekir, F fonksiyonu f fonksiyonunun ters türevidir, bir diğer deyişle F fonksiyonunun türevi f'dir.
İntegral fizikteki hız, ivme, yol, elektriksel alan, ağırlık merkezi, elektrik potansiyeli, akım şiddeti ve çoğu enerji hesaplamalarında; temel mühendisliklerin hepsinde, ekonomi ile alakalı üniversite bölümlerinde aktif olarak kullanılmaktadır. Daha da günlük yaşamdan bir örnek isteyenler olursa şu örnek verilebilir; içtiğimiz çoğu içeceğin tasarlanma şekli market dolaplarında maksimum sayı minumum hacim şeklinde integral ile hesaplanır.




















